Dans cet article, vous allez découvrir la puissance des intérêts composés !
Les intérêts composés sont l’un des mécanismes clés de l’enrichissement. Sur un investissement à long terme, les effets vertueux des intérêts composés permettent à un épargnant ordinaire de capitaliser des montants colossaux. Et cela, même avec un effort d’épargne limité comme nous allons le voir dans cet article.
C’est l’effet boule de neige : le capital génère des intérêts et les intérêts génèrent eux-mêmes des intérêts, donc le capital grossit de plus en plus vite au fil du temps.
Si vous êtes un jeune actif, savoir tirer parti des intérêts composés le plus tôt possible vous permettra d’envisager une (riche) retraite anticipée. Mais pour cela, encore faut-il comprendre le principe des intérêts composés et surtout, savoir comment optimiser ses placements pour accélérer la croissance de son patrimoine.
Certaines enveloppes d’épargne, de par leur absence de « frottements fiscaux », permettent d’optimiser l’effet boule de neige des intérêts composés.
Nous vous présentons la définition et le calcul des intérêts composés. Et nous vous présentons également plusieurs formules des intérêts composés permettant d’appréhender différents cas de figure.
Par exemple, vous êtes nombreux à vouloir savoir comment calculer :
- le capital atteint par un investissement profitant des intérêts composés avec versement mensuel (cas de l’épargnant dans la phase de capitalisation).
- l’évolution d’un capital profitant des intérêts composés avec retrait mensuel (cas de l’épargnant à la retraite).
SOMMAIRE
- Définition des intérêts composés : le principe général
- Calcul des intérêts composés : la formule
- PEA et assurance vie : 2 enveloppes pour profiter pleinement des intérêts composés
- Intérêts composés sur les actions du S&P 500
- Intérêts composés avec versement mensuel
- Intérêts composés avec retrait mensuel
- Albert Einstein et les intérêts composés
- Diversifier son capital sur plusieurs placements diminue l’effet des intérêts composés ?
Définition des intérêts composés : le principe général
Avant de plonger dans les formules de calcul des intérêts composés, explicitons sous une forme littéraire la définition des intérêts composés.
Les intérêts composés décrivent la propriété d’un investissement à se valoriser dans le temps grâce au réinvestissement des gains tirés dudit investissement sur ce dernier.
Par exemple, un investisseur peut décider de réinvestir en actions les dividendes perçus de ces mêmes actions.
Un exemple concerne le cas d’un épargnant investissant en fonds euro au sein d’une assurance vie. L’assureur (qui gère le fonds) lui verse chaque année des revenus de ce placement. Ces revenus sont automatiquement réinvestis sur le fonds euro.
Ainsi, le capital investi grossit année après année. De fait, à rendement équivalent, les gains perçus chaque année progressent dans les mêmes proportions que le capital.
La puissance des intérêts composés découle du fait que l’évolution du capital suit une progression exponentielle. Ce qui conduit (c’est mathématique) à une augmentation du capital en valeur absolue de plus en plus forte année après année.
S’il fallait imager en une phrase la définition des intérêts composés : le mécanisme des intérêts composés explique pourquoi « plus on est riche, plus on est riche« .
Jeune actif, vous pouvez espérer partir en retraite avec 1,46 million d’euros en contrepartie d’un capital initial de 15 000 € puis d’un effort d’épargne de 500 euros par mois investis sur des fonds actions (trackers).
Vous êtes peut-être dubitatif devant le montant du patrimoine atteignable. Et pourtant, vous allez voir, formule mathématique de calcul des intérêts composés à l’appui, que cet objectif est tout à fait réaliste.
Calcul des intérêts composés : la formule
Comment calculer des intérêts composés ? Ce sont des mathématiques financières basiques, niveau collège (mais il faut se rafraichir un peu la mémoire !)
Une suite géométrique
Admettons que vous ayez un capital initial K0 de 1000 euros. Ce capital est investi sur un placement délivrant une performance de 7 % par an.
Au bout d’1 an, le capital obtenu (K1) sera égal à K0 x (1 + 7 %), soit 1 070 euros.
Au bout de 2 ans, le capital obtenu (K2) sera égal à K1 x (1 + 7 %), soit 1 145 euros.
On peut également écrire que le capital obtenu au bout de 2 ans sera égal à :
K0 x (1 + 7 %) x (1 + 7 %)
En mathématique, c’est ce que l’on appelle une suite géométrique. On peut facilement calculer la valeur du capital au bout de 1, 2, 3, n années :
K1 = K0 x (1 + 7 %)
K2 = K0 x (1 + 7 %)2
K3 = K0 x (1 + 7 %)3
Etc.
À partir de là, on déduit facilement la formule des intérêts composés, ou plus exactement la formule calculant la valeur future d’une épargne profitant des intérêts composés.
La formule des intérêts composés
Pour calculer la valeur d’un investissement au bout d’un temps t (nombre d’années), la formule des intérêts composés est :
Kt = K0 x (1 + r)t
Le capital final (Kt) est égal au capital initial placé (K0) multiplié par le terme « 1 + le rendement annuel » porté à la puissance t. « t » étant le nombre d’années de l’investissement.
Gardez en tête que c’est une formule théorique. En effet, très peu de placements délivrent un rendement parfaitement stable sur de longues périodes.
La progression du capital suit une croissance exponentielle. Ses effets sur le long terme sont tout particulièrement impressionnants comme nous allons le voir plus loin, avec le cas d’un placement en bourse sur le S&P 500 avec réinvestissement des dividendes sur l’indice.
Exemple de calcul du capital final avec la formule des intérêts composés
Soit un capital initial de 100 000 euros placés pendant 10 ans à un rendement de 7 %. On applique la formule :
Capital final = 100 000 € x (1 + 0,07)10 = 196 715 €
Le capital final après 10 ans sera de 196 715 €.
Voyons à plus long terme maintenant. Quel sera le capital au bout de 30 ans ?
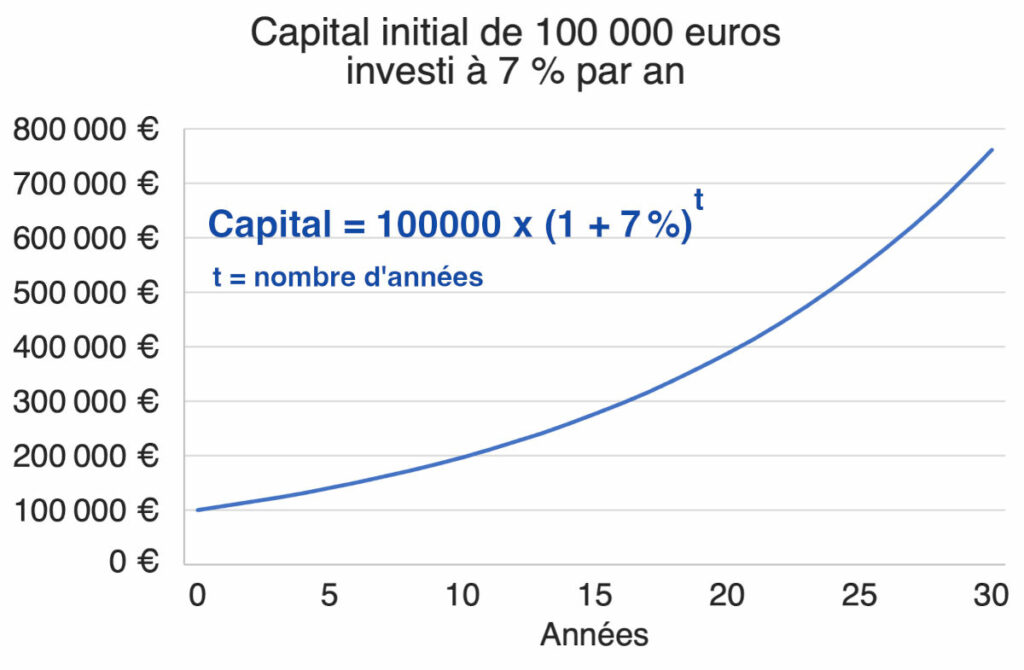
La patience paie ! Le capital a été multiplié par pratiquement 8 en 30 ans.
100 000 x (1 + 0,07)30 = 761 225 €
Le capital final sera de 761 225 €.
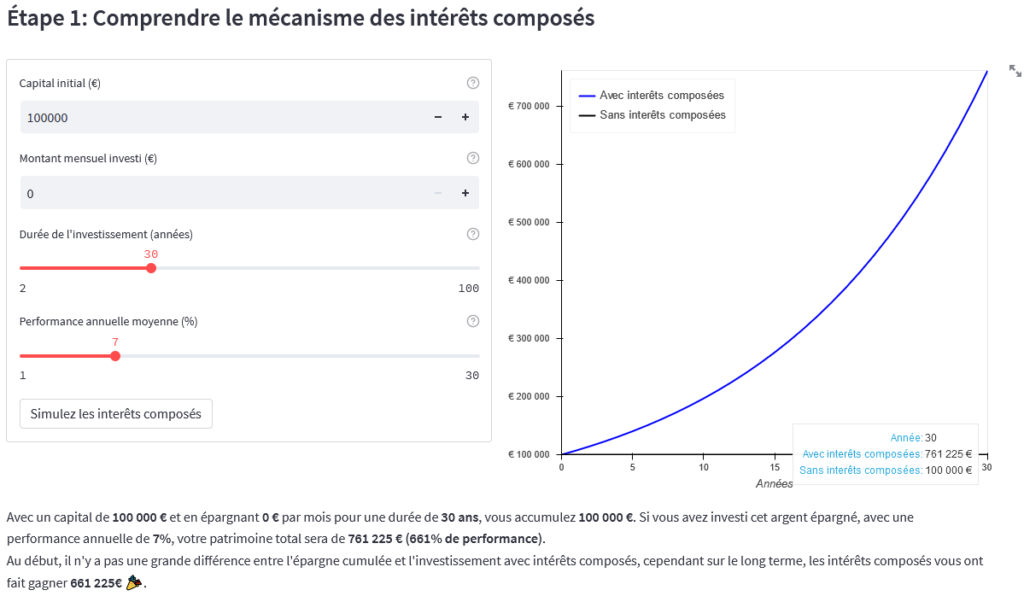
Note de Nicolas : Ludovic est un matheux, il a développé les formules puis réalisé les calculs sur Excel. Personnellement, j’utilise le simulateur d’Othmane (un lecteur d’ADI très talentueux !). C’est un outil très pratique, dans mes liens favoris car je l’utilise souvent ! On voit ci-dessous que ça colle avec le calcul de Ludovic : même résultat de 761 225 € après 30 ans.
Doubler son capital tous les 10 ans
Avec un rendement moyen annuel de 7,18 %, et grâce aux intérêts imposés, un investisseur double la valeur de son investissement tous les 10 ans.
D’où sort ce chiffre ? Pour déterminer le rendement (r) de 7,18 %, il suffit de résoudre l’équation 2 = (1 + r)10. Que l’on peut aussi écrire sous cette forme :
r = 21/10 – 1
Il se trouve que la performance des marchés actions est à peu près de cet ordre sur le long terme (elle est même un peu supérieure sur certaines décennies). L’indice MSCI World a dépassé les 10 % de performance annualisée sur 2011-2021 (cf ETF World).
Un épargnant qui placerait 100 000 € sur un fonds en actions capitalisant, oublierait son compte, et s’y connecterait 50 ans plus tard verrait la valorisation de son investissement avoisiner les 3,2 millions d’euros. Un beau cadeau pour ses héritiers…
Exemple pour 100 000 € investis à 30 ans
Admettons que vous placiez 100 000 € à l’âge de 30 ans, à 7,18 %, le capital va doubler tous les 10 ans :
- 30 ans = 100 000 € ;
- 40 ans = 200 000 € ;
- 50 ans = 400 000 € ;
- 60 ans = 800 000 € ;
- 70 ans = 1 600 000 € ;
- 80 ans = 3 200 000 € ;
- 90 ans = 6 400 000 € ;
- 100 ans = 12 800 000 €.
Vous aurez environ 12 millions d’euros de capital quand vous serez centenaire.
Vous ne serez probablement pas assez en forme pour en profiter (sauf si la médecine fait de gros progrès !) mais vous comprenez la force des intérêts composés à long terme, pourquoi Warren Buffett est devenu si riche en investissant plus de 70 ans, et pourquoi les vampires sont souvent de riches rentiers !
Note de Nicolas : dans la vie réelle, vous auriez sans doute craqué tôt ou tard sans laisser filer les intérêts composés pendant 70 ans. Car vous ne voulez peut-être pas être le plus riche du cimetière. Vous auriez peut-être profité du capital à 40 ans pour acheter une Porsche à 200 000 €, ou à 60 ans pour acheter une résidence secondaire à 800 000 €, ou à 70 ans pour faire des donations à hauteur de 1,6 M€ à vos enfants et petits-enfants. L’épargne est généralement de la consommation différée, pour s’offrir bien plus qu’avec le capital d’origine.
Gare à l’imposition
Ce calcul ne tient pas compte des taxes et des impôts. Or, la plupart des revenus de placements sont imposables.
Par exemple, si vous investissez via un compte-titres ordinaire, les dividendes sont imposables. Donc la performance du placement et la formule des intérêts composés doit donc tenir compte de cette taxation des gains au fil de l’eau.
La bonne nouvelle est qu’il existe des placements ne supportant pas d’imposition au cours de la phase de capitalisation de l’épargne ! Ce sont les enveloppes capitalisantes.
PEA et assurance vie : 2 enveloppes pour profiter pleinement des intérêts composés
Les intérêts composés sont un phénomène d’autant plus puissant que l’épargnant est en mesure de réinvestir la totalité des gains chaque année.
Exemple chiffré
Pour s’en convaincre, prenons le cas d’un capital initial de 10 000 euros investis sur un placement rapportant 7 % pendant 20 ans. Le graphique ci-dessous présente la progression du capital en présence et en l’absence d’une imposition annuelle des gains (« frottement fiscal »).
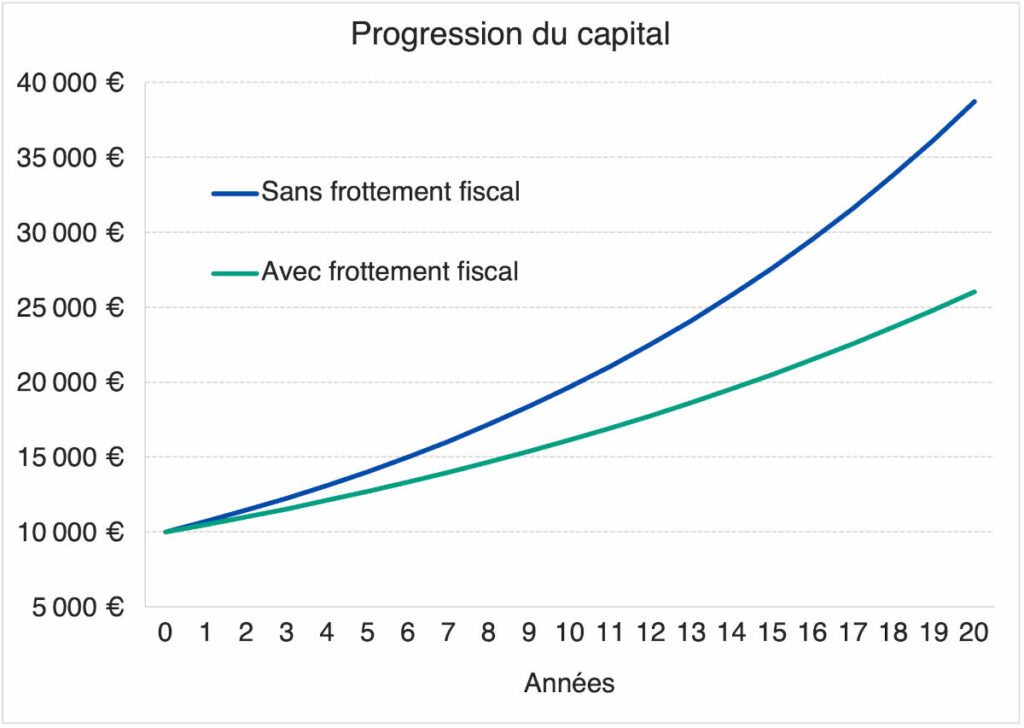
Dans le 1er cas (courbe verte), les revenus supportent une imposition annuelle des gains à 30 % (c’est le cas de la flat tax appliquée sur les dividendes et d’autres revenus de valeurs mobilières). Le rendement net annuel est de 4,9 % (7 % – 30 % = 4,9 %). Le capital final est de 26 032 euros, soit une plus-value de 16 032 euros.
Dans le second cas (courbe bleue), en l’absence de frottement fiscal, l’effet des intérêts composés tourne à plein régime. Le capital final est de 38 697 euros, soit une plus-value latente de 28 697 euros. Admettons que la plus-value supporte une imposition au moment où l’épargnant sort son capital après 20 ans. Auquel cas, même après imposition des gains de 30 % (30 % de 28 697 euros), le capital final net d’impôt est de 30 088 euros.
En l’absence de frottement fiscal, l’effet vertueux des intérêts composés permet de capitaliser beaucoup plus ! Pour cette raison, il est judicieux de se tourner vers des placements permettant de limiter au maximum les frottements fiscaux.
Les placements optimisés fiscalement
Les dividendes perçus sur un compte-titres ordinaire (CTO) sont taxés à hauteur de 30 %. En l’absence d’optimisation, les revenus de SCPI ou d’investissements immobiliers en direct peuvent supporter des niveaux d’imposition par défaut encore supérieurs.
Pour optimiser la progression de son épargne, l’épargnant doit donc mettre en place une stratégie permettant de réinvestir le maximum des gains réalisés au fil de l’eau.
Du côté des placements financiers, il faut privilégier le PEA et l’assurance vie :
- Le PEA permet d’investir en actions.
- L’assurance vie permet d’investir sur des fonds actions (dont les trackers et ETF), mais également sur des SCPI (voir notre article sur les SCPI en assurance vie).
Le PEA et l’assurance vie se distinguent par une absence de frottement fiscal et une imposition réduite des plus-values à la sortie en optimisant les retraits : 17,2 %. Tant que l’on reste dans l’enveloppe, même en cas de dividendes perçus et de plus-values réalisées, il n’y a pas d’imposition.
Si l’on reprend l’exemple cité plus haut de l’épargnant investissant 10 000 euros sur un placement rapportant 7 % par an sur 20 ans : le capital final net d’impôts et taxes sera de 33 761 euros !
En résumé : bien profiter des intérêts composés
Les placements supportant une imposition au fil de l’eau sont les moins intéressants (en particulier en phase de capitalisation). Car l’effet des intérêts composés est freiné par l’imposition.
Les placements ne supportant pas d’imposition au fil de l’eau profitent pleinement de l’effet vertueux des intérêts composés. C’est par exemple le cas des fonds actions capitalisants (voir en bas de cet article : ETF répliquant le MSCI World) que l’on peut loger dans un compte-titres ordinaire (CTO). Mais attention, avec un CTO, en cas de cession des parts, la plus-value sera taxable.
Sachez que la cession des parts de fonds peut être contrainte si ce dernier est délisté par la société de gestion. C’est assez rare mais cela peut arriver, pour cette raison il faut privilégier des fonds généralistes plutôt que des fonds thématiques et/ou trop spécialisés.
L’idéal en termes de stratégie patrimoniale est de profiter d’une enveloppe capitalisante telle que le PEA, l’assurance vie ou encore le PER pour combiner les 2 avantages :
- l’absence de frottements fiscaux au cours de la phase de capitalisation ;
- une imposition réduite à la sortie (ou l’avantage fiscal à l’entrée dans le cas du PER).
Les avantages fiscaux tiennent compte de la date d’ouverture des enveloppes (et non la date des investissements). Vous avez donc intérêt à ouvrir un PEA, une assurance vie et un PER le plus tôt possible.
Nous vous renvoyons à nos sélections comparatives des meilleurs acteurs :
- des meilleurs PEA,
- des meilleures assurances vie,
- et des meilleurs PER.
Intérêts composés sur les actions du S&P 500
Pour mesurer à quel point les intérêts composés sont un mécanisme puissant pour devenir riche (n’ayons pas peur des mots quand il s’agit d’appréhender des processus exponentiels !), on peut se référer au cas d’un épargnant investissant sur le marché actions américain au travers du S&P 500.
Dans le cas des actions, pour profiter de l’effet vertueux des intérêts composés, il suffit de réinvestir année après année les dividendes perçus.
Pour suivre l’évolution du capital investi sur le S&P 500 en réinvestissant les dividendes sur l’indice, nous n’avons pas besoin de faire de calcul, il suffit de se référer à la performance « total return » de l’indice S&P 500 TR. Cet indice suit la performance de l’indice, en tenant compte du réinvestissement des dividendes des actions qui composent l’indice.
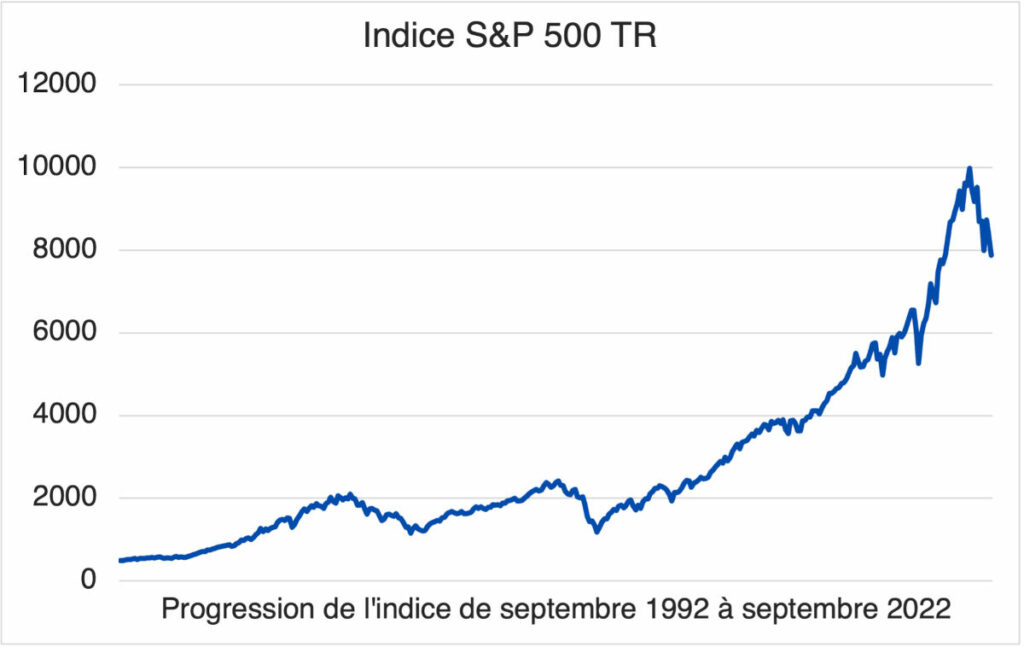
Source : Yahoo Finance
Le S&P 500 TR a clôturé à 491 points le 1er septembre 1992. 30 ans plus tard, le 1er septembre 2022, il a clôturé à 7 965 points. Soit une multiplication par plus de 16 de l’indice. Exprimée en pourcentage, la hausse est de 1520 % !
Quelle est la performance annualisée de l’indice ?
Valeur finale / valeur initiale = 7965 /491 = 16,20976.
On doit résoudre l’équation suivante (maths niveau BAC) :
16,20976 = (1 + r)30
Pour déterminer « 1+r », il suffit de porter 16,20976 à la puissance 1/30 :
16,20976(1/30) = 1,097301.
La performance annuelle moyenne du S&P 500 TR entre le 1er septembre 1992 et le 1er septembre 2022 a donc été de 9,7 %.
Dans nos outils, vous trouverez le lien vers un simulateur.
Intérêts composés avec versement mensuel
Il peut être utile de connaître non pas la performance annuelle, mais la performance mensuelle. C’est notamment le cas pour suivre la progression d’une épargne alimentée chaque mois. Il faut alors calculer les intérêts composés mensuellement.
La formule de calcul des intérêts composés avec versement mensuel est :
Kf = K0 x (1 + i)n + [E x ( (1 + i)n – 1) / i]
Cette formule est la somme de 2 termes. Le premier terme est celui que nous avons vu précédemment, il calcule la part du capital final (Kf) obtenu à partir du capital initial (K0).
Le second terme de l’expression permet de calculer la part du capital final (Kf) obtenu à partir des versements mensuels (E).
E : l’effort d’épargne mensuel (le capital placé en fin de mois).
i : le taux d’intérêt (la performance) mensuelle.
n : le nombre de mois.
Si le capital initial K0 est nul (l’épargnant démarre sans capital initial), la formule se simplifie :
Kf = E x ( (1 + i)n – 1) / i
Généralement, on raisonne en termes de performance (ou de rendement) annuelle et non mensuelle. Pour obtenir la performance mensuelle, vous pensez peut-être qu’il suffit de diviser par 12 la performance annuelle ? Ce n’est pas forcément le cas ! Explication.
Comment déterminer la performance mensuelle à partir de la performance annuelle ?
Cela dépend du type de placement.
Cas d’un livret
Pour ce qui est des livrets réglementés (livret A et LDDS) : les intérêts ne sont versés qu’à la fin de l’année. Les intérêts générés en cours d’année ne s’agrègent pas au capital placé au fil des mois.
Le taux d’intérêt mensuel s’obtient en divisant le taux d’intérêt annuel par 12. Ici, il n’y a pas de piège.
Note au passage : il faut également savoir que les intérêts sont validés par quinzaine (un versement réalisé sur le livret le 8 du mois ne commencera à produire des intérêts qu’une semaine plus tard).
Cas de la performance des marchés actions
Pour les marchés actions, le calcul de la performance mensuelle est différent de celui d’un livret. En effet, la progression de la valeur des actions et des portefeuilles se fait de façon continue dans le temps. Les entreprises réinvestissent leurs gains tout au long de l’année, elles n’attendent pas la fin de l’année pour allouer le capital. Money Never Sleeps…
Pour calculer la performance mensuelle à partir de la performance annuelle, on peut reprendre la formule des intérêts composés présentée plus haut et l’adapter à cette question.
Soit un capital initial K0 (en début d’année), un capital final Kf (en fin d’année, 12 mois plus tard), un rendement annuel de r (en %), et un rendement mensuel i (en %) que l’on cherche à déterminer.
On pose les équations :
Kf = K0 x (1 + r),
Kf = K0 x (1 + i)12 (il y a 12 mois dans une année…),
Donc K0 x (1 + r) = K0 x (1 + i)12,
Cette expression se simplifie : (1 + r) = (1 +i)12.
Donc i = (1 + r)(1/12) -1
Vous savez désormais comment calculer la performance mensuelle moyenne des marchés actions à partir de la performance annuelle.
Exemple de calcul de performance mensuelle à partir de la performance annuelle
On prend le cas d’un placement en actions donc la performance annuelle est de 9 %.
La performance mensuelle moyenne (i) est égale à (1 + 9%)(1/12) -1. Ce qui donne une performance mensualisée de 0,72 % (0,7207323 % pour être plus précis).
Cas d’un épargnant plaçant 300 euros par mois
Voyons maintenant le cas concret avec un épargnant démarrant avec un capital nul et plaçant 300 euros par mois (en fin de mois, au moment de toucher son salaire). Pendant 20 ans (240 mois) sur un placement en actions rapportant en moyenne 7 % par an.
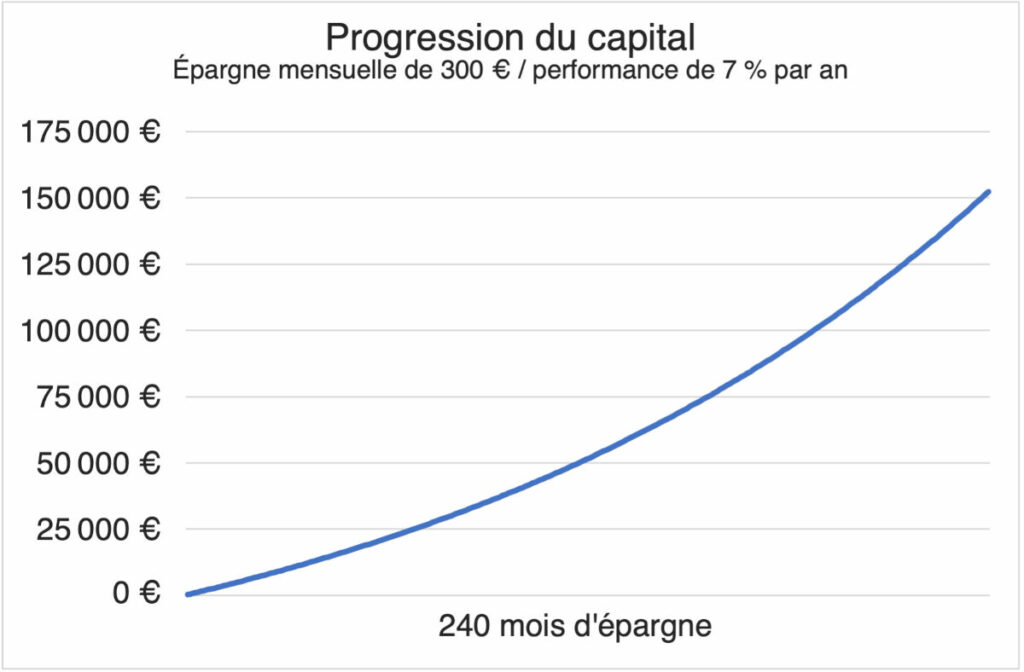
La performance moyenne mensuelle est égale à 0,5654 %. Nous avons appliqué la formule : (1 + 7%)(1/12) – 1
Le capital final sera de 152 258 euros.
Pour calculer ce montant, on applique la formule donnée plus haut :
300 € x ((1 + 0,5654 %)240 – 1) / 0,5654 %. (240 mois en 20 ans).
Les simulateurs en ligne ne donnent pas tous exactement les mêmes résultats. Or erreur, cela tient généralement au fait que les méthodes de calcul peuvent différer, notamment sur les 2 points suivants :
- l’épargne mensuelle est-elle investit en début ou en fin de mois ?
- comment le simulateur détermine-t-il le rendement mensuel à partir du rendement annuel renseigné par l’internaute ? (Idéalement, il faut distinguer le cas des placements dont les gains sont servis en fin d’année de ceux servis tout au long de l’année).
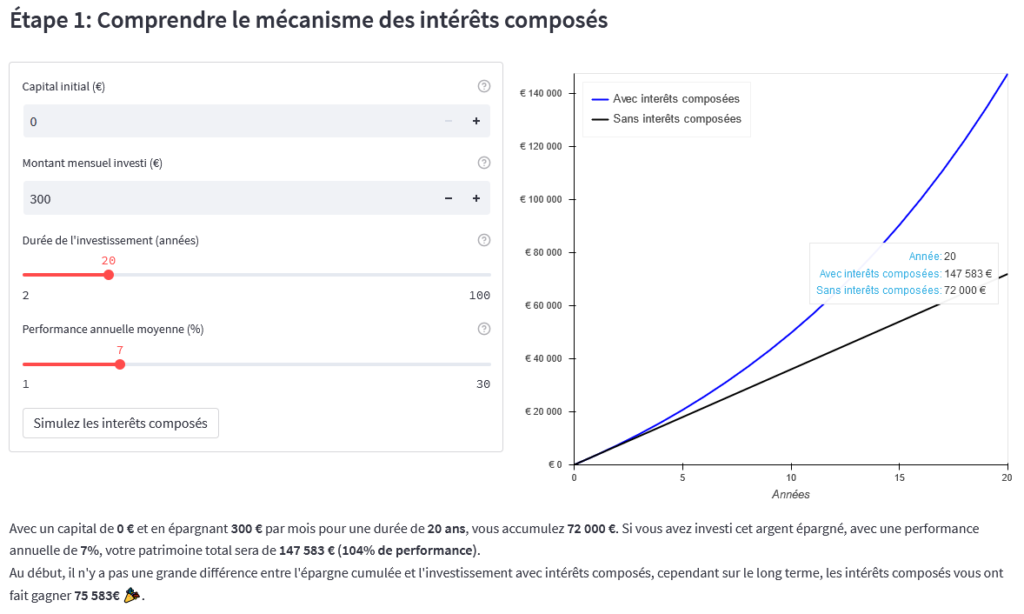
Note de Nicolas : c’est le cas ici avec le simulateur d’Othmane. On voit ci-dessous que ça ne colle pas tout à fait avec le calcul de Ludovic : résultat de 147 583 € après 20 ans, alors que Ludovic trouve 152 258 € avec la formule. Ceci dit on est dans le même ordre de grandeur, environ 150 k€. Cela vient du fait que le simulateur d’Othmane capitalise à la fin de l’année et non mensuellement. Une capitalisation mensuelle fait naturellement grossir davantage le capital.
Devenir millionnaire avec les intérêts composés
Nous avons évoqué plus haut dans cet article le cas d’un épargnant parvenant à capitaliser 1,46 million d’euros pour sa retraite.
Vous connaissez désormais la formule pour vérifier cette projection !
Pour rappel, notre jeune épargnant dispose d’un capital initial de 15 000 euros, et place 500 euros par mois sur un fonds actions délivrant une performance annuelle moyenne de 7 %. Il capitalise pendant 40 ans (480 mois) avant de partir en retraite.
Le calcul :
15 000 x (1 + 0,5654 %)480 + 500 x ( (1 + 0,5654 %)480 – 1) / 0,5654 %
Ce qui nous donne bien 1,46 million d’euros. Avec un effort d’épargne mensuel à la portée de bon nombre d’épargnants, on peut effectivement devenir millionnaire avec les intérêts composés.
Intérêts composés avec retrait mensuel
Le cas des intérêts composés avec retrait mensuel est un cas de figure courant. Il concerne les épargnants en phase de « désépargne », autrement dit en phase de consommation. C’est souvent le cas des retraités.
Calculer l’évolution du capital en tenant compte à la fois des intérêts composés et du retrait mensuel permet d’anticiper le capital futur et de mesurer à quelle vitesse le capital va se consommer (dans le cas où les retraits sont supérieurs aux intérêts).
D’un mois sur l’autre, le capital évolue de la façon suivante suivant :
K(n+1) = K(n) x (1 + i) – E
où E est le montant du retrait réalisé à la fin de chaque mois. Les autres termes ont déjà été explicités plus haut (n le mois et i le rendement mensuel).
Les plus observateurs auront ici reconnu une fonction affine, c’est-à-dire de la forme y = ax + b.
K(n+1) = K(n) x (1 + i) – E est une expression de la forme y = ax + b
Connaissant le capital initial, le rendement mensuel et le montant du retrait mensuel, on peut déterminer le capital final après n mois en résolvant la suite arithmético-géométrique correspondante.
Je vous passe les détails du calcul (calcul du point fixe, etc.). La formule permettant de calculer le capital (Kn) à l’horizon n mois en fonction du capital initial (K0), du rendement (i) et du montant des retraits mensuels (E) est :
K(n) = (1 + i)n x (K0 – E/i) + E/i
Exemple
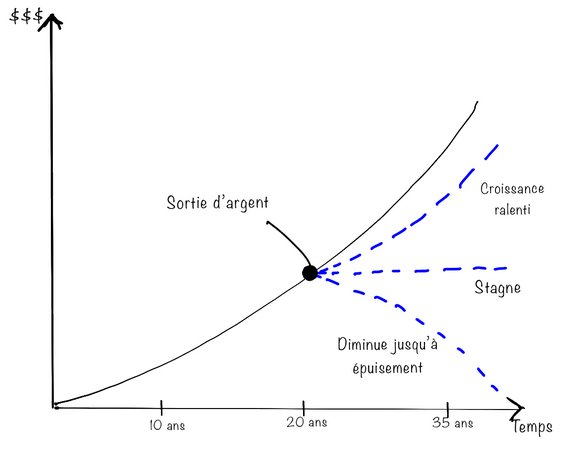
Un épargnant dispose de 100 000 euros sur un fonds diversifié dont la performance moyenne annuelle est de 6 %. Il réalise un retrait partiel de 500 euros à chaque fin de mois.
La performance mensuelle est de (1 + 6 %)(1/12) -1 = 0,4867551 %
Quel sera le capital restant au bout de 10 ans (120 mois) ?
K(120) = (1 + 0,4867551 %)120 x (100 000 – 500/0,4867551 %) + 500/0,4867551 % = 97 848 euros
10 ans plus tard, le capital est donc proche du capital initial. Cela s’explique tout simplement par le fait que le retrait mensuel (500 euros) est très proche du gain mensuel (la performance mensuelle de 0,487 % délivre une rente de 487 euros). Les flux entrants et sortants sont presque à l’équilibre.
Et si l’épargnant réalise un retrait partiel de 600 euros à la fin de chaque mois ? Le résultat est très différent. En effet, au bout de 10 ans (120 mois), le capital restant sera de 81 601 euros. L’érosion du capital va en s’accélérant à mesure que le capital se réduit dans le temps. Ainsi, au bout de 20 ans, avec des retraits de 600 euros par mois, le capital restant ne sera que de 48 650 euros.
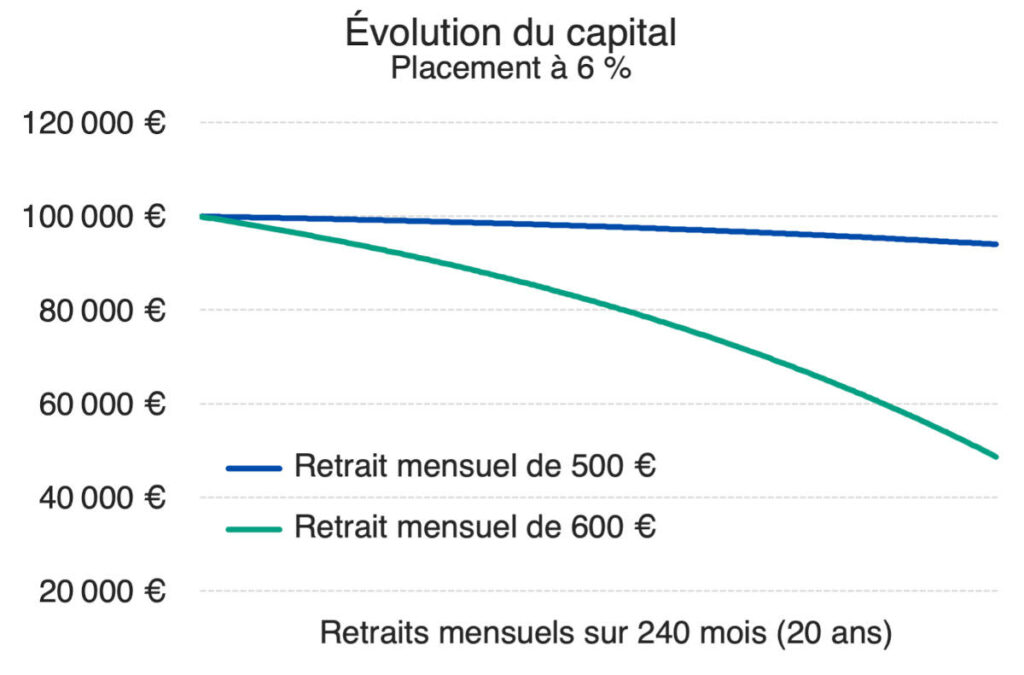
Si vous prévoyez de battre le record de longévité de Jeanne Calment, vous avez intérêt à être particulièrement attentif aux montants des retraits mensuels que vous pouvez vous autoriser pour ne pas éroder trop rapidement votre capital !
Note de Ludovic : ces calculs ne tiennent pas compte de l’inflation. À ce sujet, je vous renvoie à notre article présentant les solutions pour protéger son épargne de l’inflation. Rappelons encore une fois ici que c’est un modèle théorique, il n’existe pas de fonds diversifié délivrant une performance parfaitement stable sur de longues périodes, la volatilité est certaine.
Albert Einstein et les intérêts composés
Pourquoi Albert Einstein figure-t-il dans l’image d’illustration de cet article consacré aux intérêts composés ?
Albert Einstein aurait déclaré : « les intérêts composés sont la huitième merveille du monde. Celui qui le comprend s’enrichit ; celui qui ne le comprend pas, le paie « . C’est en tout cas ce que l’on peut lire sur internet… L’information, largement relayée, est à prendre avec des pincettes, cette déclaration n’est pas confirmée.
En revanche, la force des intérêts composés, elle, est incontestable !
Diversifier son capital sur plusieurs placements diminue-t-il l’effet des intérêts composés ?
Des internautes nous partagent quelquefois une inquiétude reposant sur une mauvaise compréhension du principe des intérêts composés. Voici le genre de message que l’on reçoit parfois :
« Je redoute un peu de séparer mon argent sur plusieurs assurances vie, car si je veux pouvoir profiter au mieux des intérêts composés il ne faudrait pas que je sépare cette somme. »
Faux !
Comme nous l’avons vu dans cet article, la formule permettant de suivre l’évolution d’un capital K investi au rendement r (annuel) sur une durée de t (en années) est :
K = K0 x (1 + r)t
Le capital initial (K0) peut être fractionné sur plusieurs contrats sans incidence sur la valeur totale du capital K. Les intérêts composés courent sur chaque contrat.
Par exemple, dans le cas d’un contrat avec 1 000 euros initialement et un rendement annuel de 5 %, au bout de 10 ans, on obtient 1 000 x (1 + 5 %)10 = 1 629 euros.
Si l’épargnant ouvre 3 contrats avec 1 000 euros sur chacun, cela donne 4 887 euros.
Et s’il place sur un seul contrat 3 000 euros avec les mêmes conditions (un rendement de 5 %), il obtient également 4 887 euros au bout de 10 ans :
3 000 x (1 + 5 %)10 = 4 887 €.
Les bonnes raisons d’ouvrir plusieurs contrats
Nous avons vu que la multiplication des contrats et enveloppes (assurance vie, PEA, PER…) est sans incidence sur l’effet vertueux des intérêts composés.
A contrario, il existe de bonnes raisons de multiplier les enveloppes :
Un PEA
Le PEA est spécifiquement pensé pour investir en actions et les plus-values sont imposées à taux réduit (seulement les prélèvements sociaux : 17,2 %) à la sortie d’un PEA de plus de 5 ans. Malheureusement il y a un plafond de versement de 150 000 €.
Plusieurs assurances vie
Par ailleurs, l’assurance vie est un dispositif ultra-souple et multi-projet. L’argent est disponible à tout moment et l’épargnant peut utiliser l’enveloppe pour différents projets de vie (préparer un achat immobilier, développer son patrimoine, préparer sa retraite, etc.).
L’assurance vie permet de diversifier son patrimoine sur plusieurs types de placements (du plus sécurisé comme le fonds euro aux plus dynamiques comme les fonds actions ou matières premières, en passant par l’immobilier).
Il est d’ailleurs recommandé d’ouvrir plusieurs assurances vie pour combiner les avantages respectifs des meilleures assurances vie (certaines s’illustrent par l’offre de fonds actions, d’autres par le choix de supports immobiliers ou la performance de leur fonds euro). Pourquoi diversifier sur plusieurs assurances vie.
C’est aussi une niche fiscale : exonération d’impôt sur le revenu possible en sortant après les 8 ans de l’assurance vie, et transmission de capital exonérée de droits de succession à hauteur de 152 500 € par bénéficiaire.
Et éventuellement 1 ou 2 PER
Le plan épargne retraite (PER) est spécifiquement pensé pour préparer sa retraite. C’est un placement à la fois simple à utiliser et très efficace pour diminuer son impôt sur le revenu. Particulièrement recommandé pour les contribuables en tranche marginale d’imposition 30 % et plus, en complément de l’assurance vie.
L’offre de fonds d’investissement sur PER est la même que celle disponible en assurance vie.
Passez à l’action : épargnez en profitant des intérêts composés
PEA, assurance vie et PER ont un point commun : l’absence de frottement fiscal tant que l’épargnant reste dans l’enveloppe. C’est une caractéristique essentielle pour optimiser l’effet vertueux des intérêts composés.
Nos articles à lire pour aller plus loin et investir sur les meilleurs placements pour profiter des intérêts composés :
- les meilleurs PEA,
- les meilleures assurances vie,
- et les meilleurs PER.
32 commentaires sur “Intérêts composés : calcul et formules du secret pour s’enrichir”
Bonjour Nicolas,
Merci pour tout votre travail, je ne pensais pas me passionner autant pour ces sujets qui pour moi étaient si obscurs il y a encore quelques semaines !
Je me joins à ces commentaires pour que vous me confirmiez si j’ai bien compris cette notion d’intérêts composés appliquée aux actions (et pourquoi pas pour que ça aide, car je pense voir d’où vient la confusion). Dans le cas où des intérêts sont perçus chaque année c’est limpide. Mais prenons l’exemple d’une action qui aurait pris 140% en 20 ans, est-il faux de dire que sa performance moyenne annuelle est de 7% ? La performance moyenne annuelle serait plutôt ((1+1,40)^(1/20)) – 1 = 4,47%.
Est-ce qu’alors quand on lit partout « le marché des actions a une performance historique d’une moyenne de 7% /an », on peut aussi comprendre : « le marché des actions a en moyenne augmenté de 287% ces 20 dernières années » ?
Merci d’avance pour vos explications !
Bonjour Camille,
Vous avez compris, une performance annuelle de 7 % par an ça ne fait pas +70 % mais environ + 100 %, on double le capital 🙂
Et sur 20 ans on quadruple presque le capital (+287 % en effet).
Et +140 % en 20 ans, c’est seulement +4,47 % de performance annualisée et non +7 %.
Bonjour Nicolas,
Je suivais récemment votre PEA que vous aviez gentiment publié pour nous 🙂
Vous possédiez 2 ETF WORLD sur PEA.
Sur un PEA, qu’on ait 100 000€ investis sur un seul ETF World capitalisant ou 100 000€ investi sur 2 ETF WORLD capitalisant, il n’y a aucune différence au niveau des performances et des intérêts composés ?
On est bien d’accord que c’est le capital investi au total qui joue sur les intérêts composés. Peu importe le support d’investissement ? Je me trompe ?
Je pose cette question car il y a le nouvel ETF d’IShares (WPEA) qui vient d’arriver sur le marché des PEA.
J’hésitais donc entre arrêter mon DCA sur CW8 et passer sur WPEA (et ainsi avoir 2 ETF en portefeuille) ou vendre CW8 pour tout mettre sur WPEA et par la suite, continuer mon DCA sur WPEA. (1 ETF en portefeuille)
Merci
Thomas
Bonjour Thomas,
« Sur un PEA, qu’on ait 100 000€ investis sur un seul ETF World capitalisant ou 100 000€ investi sur 2 ETF WORLD capitalisant, il n’y a aucune différence au niveau des performances et des intérêts composés ? »
=> Tout à fait !
Moi-même je compte investir également sur WPEA maintenant pour diversifier l’émetteur (iShares plutôt que Amundi).
Je vous invite à lire le paragraphe sous le 1er graphique de cet article : https://avenuedesinvestisseurs.fr/questions-reponses-finance-personnelle/
Sur le sujet des intérêts composés, une formule assez simple à retenir : le capital inital double double tous les [70 / taux] ans.
Ex, j’investis 10k€ aujourd’hui à un taux théorique constant de 7% par an, j’aurais doublé mon capital dans 70/7 = 10 ans
Oui bien vu, c’est mon moyen rapide pour calculer 🙂
Bonjour,
Cet article est très complet et très intéressant.
Vous expliquer qu’on peut placer notre argent par exemple en assurance vie, en S & P 500 ou en PER mais où, sur quelle plateforme?
Et je me demande aussi comment on est assuré que nos investissent sont placé avec intérêt composé et non sans intérêt composé, quelle démarches devons-nous faire?
Merci pour toutes ces informations.
Bonjour Héloise,
C’est simple, sur les meilleures assurances vie.
Et les meilleurs PER.
(Cliquez sur les liens, vous verrez nos classements).
Sur assurance vie et PER, on profite nécessairement des intérêts composés tant qu’on investit à long terme.
Bonjour,
Est-ce qu’il existe des assurances vie qui versent les bénéfices tous les mois voire tous les jours ? Afin d’avoir des intérêts composés quotidiens.
Merci !
Bonjour Adrien,
L’assurance vie est une enveloppe d’investissement, tout dépend comment vous investissez dedans :
– fonds euro = intérêts versés en janvier N+1 ;
– SCPI = loyers versés tous les trimestres ;
– fonds actions capitalisant (ETF) = la valeur évolue tous les jours.
Etc.
Notre article : l’assurance vie.
Merci pour cet article encore très instructif. J’ai cependant une question. J’aimerais comparer deux portefeuilles d’ETF et l’incidence des frais avec un DCA mensuel. En lisant le DIC des ETF, on voit que les frais de X% sont sur l’encours total à la fin de l’année.
J’ai beaucoup de mal à voir comment intégrer ces frais de gestion dans le calcul Kf = E x ( (1 + i)^n – 1) / i. En effet, si je fais Kf = E x ( (1 + i)(1 – f)^n – 1) / i, je pense que cela est faux car ça ramènerait les frais sur le montant mensuel. Est-ce que par hasard vous auriez une idée ?
Peut être qu’il faudrait calculer l’encourt annuel puis appliquer la formule Kf = K0 x (1 + i)^n + [E x ( (1 + i)^n – 1) / i] avec K0 = encourt de l’année précédente * les frais ?
Merci beaucoup !
Pour intégrer les frais de gestion dans la formule : il faut utiliser la valeur de i correspondant à la performance mensuelle nette de frais.
Pour ce faire, la méthode la plus simple est de calculer la performance annuelle nette de frais, et ensuite de calculer la performance mensuelle correspondante.
Exemple dans le cas d’un placement (fonds actions) avec une performance brute annuelle de 7 % :
Si les frais de gestion annuels sont de 0,50 % par an, la performance annuelle nette de frais est de :
(1 + 7 %) x (1 – 5 %) – 1 = 6,465 % par an.
Note : une erreur classique est de soustraire 0,50 % à 7 % (= 6,50 %) pour calculer la performance annuelle nette de frais. Ce qui revient à calculer le montant des frais de gestion sur la valeur du capital en début de période (début d’année). Or, la valeur du capital (du fonds) évolue dans le temps et les frais sont collectés au fil de l’eau ! La bonne formule est celle donnée ci-dessus.
À partir de ce chiffre, vous pouvez ensuite calculer la performance mensuelle nette de frais de gestion correspondante :
(1 + 6,465 %)^(1/12) -1 = 0,5234159 % -> c’est la valeur de i que vous pouvez ainsi utiliser dans la formule de calcul du capital avec DCA mensuel.
(La formule du calcul de la performance mensuelle à partir de la performance annuelle utilisée ci-dessus est donnée dans l’article).
Merci pour cette réponse très complète. Ça parait logique en plus. Désolé de ne pas y avoir pensé !
Bonjour,
Merci vivement pour cet article.
Si j’en comprends les mécanismes, dans les faits c’est autre chose.
Imaginons, j’investis 100 sur l’ETF MSCI World. Le lendemain je serai peut-être à 103, 98 le surlendemain, 97 le jour d’après, 101 le jour encore d’après, bref ça fluctue tous les jours. Comment et quand sont calculés les intérêts ? A partir de quand, je génère des intérêts sur mes intérêts ? Si je regarde l’évolution sur 12 mois sur mon AV, le MSCI World a un progression de + 9,44%, comment cette valeur a été calculée, svp ?
Vous remerciant par avance pour votre retour.
Bonjour,
Quand vous investissez en actions (ou en fonds actions), les intérêts composés correspondent (1) au réinvestissement par les entreprises des bénéfices qu’elles génèrent et (2) au réinvestissement par l’actionnaire des dividendes qu’il perçoit.
Et si vous investissez via un fonds actions capitalisant (répliquant le MSCI World ou un autre indice), alors les intérêts composés se créent automatiquement du fait que le fonds réinvestit directement les dividendes en actions, ce qui fait d’autant plus progresser la valeur du fonds.
Merci Nicolas pour votre réponse.
Cependant, j’ai bien lu l’article proposé et cela ne m’éclaire toujours pas.
Déjà car dans cet article, vous dites je cite : « Certes recevoir des dividendes peut rassurer, comme des revenus passifs. Mais il s’agit également d’un biais psychologique contreproductif ». Bref, on touche des dividendes mais on a presque perdu autant sur l’action donc on stagne… J’en déduit donc qu’il vaut mieux éviter les dividendes.
Si je reprend mon exemple mais en imaginant alors un ETF. Valeur à l’achat 100 euros en 2020. Des montées, des descentes pendant 10 ans pour finir à une valeur de 150 euros. On se dit, ok on est à 5%/an. Mais je n’ai alors que 150 euros alors qu’avec les calculatrices d’intérêt composé, on annonce 164€. Et si la ca continu toujours sur 5%/an pendant 20 ans supplémentaire, j’aurai 250 euros alors qu’on annonce 439€ avec les intérêts composés.
Il y a un élément où je me trompe ?
Merci d’avance Nicolas.
Bonjour Ludovic, Nicolas,
Petite question sur les intérets composés, intégrant les frais de gestions, notamment dans le cadre de l’assurance vie.
Au départ notre formule : Kt = K0 x (1 + r)t – Prenons un investissement initiale sans DCA.
Pour le PEA en gestion libre, cela semble assez simple, il suffit de que le Kt intègre les frais de courtage
Par contre comment intégrer dans la formule les frais d’une assurance vie (pilotée ou non)?
Comme ça j’aurai tendance à dire:
Kt = K0 x (1 + (r-frais annuel))t
Est-ce juste?
Bonjour,
La formule intégrant les frais de gestion dépend de la façon dont ces frais sont calculés… Quelques nuances existent selon les gestionnaires, les assureurs, les fonds (prélèvement mensuel pour les uns, trimestriel pour d’autres, etc.)
La formule que vous donnez à la fin de votre message s’applique si les frais sont calculés et prélevés sur l’encours au début de l’investissement. Ce n’est généralement pas ce qui se passe. En pratique, les frais de gestion des unités de compte ou les frais de gestion pilotée sont prélevés au fil de l’eau. Pour calculer la progression du capital en intégrant les frais, il faut plutôt utiliser la formule suivante : (1 + r)(1 – f)
avec r le rendement (en %) et f les frais (en %).
Formule que vous pouvez élever à la puissance t, la durée de l’investissement (à laquelle correspond une performance r donnée) pour suivre la performance nette de frais du capital sur plusieurs mois ou années (selon l’intervalle de temps choisie) : Kt = K0 x ( (1 + r)(1 – f) )^t
Bonjour Nicolas,
Merci pour votre travail et également les différents podcast très intéressant !
Comme l’un des commentaires, j’ai une LMNP en plus de ma RP. Je souhaiterais alléger ma capacité d’emprunt, revendre ma LMNP Lilloise (plus value de 50 000€ sans l’impot) et idéalement placer cet argent pour bénéficier des intérêts composés.
J’ai déjà une assurance vie « secure » mais j’avour avoir du mal à cibler les actions S&P500 via un PEA en passant par Linxea.
Avez-vous une suggestion pour être sûr d’investir sur le bon tracker ? je trouve les plateformes peu intuitives là-dessus. Merci !
Bonjour Thib,
Merci 🙂
Si vous vendez votre appartement avec crédit en cours, vous allez au contraire diminuer votre endettement donc augmenter votre capacité d’emprunt.
Nous recommandons l’ETF World plutôt que l’ETF S&P 500, pour diversifier au mieux sur le marché actions internationales.
Le PEA Linxea est un PEA assurance et non un PEA classique…pas terrible.
On donne ici les références du tracker World sur chacune des meilleures enveloppes (PEA, assurance vie…) : comment investir en ETF World.
Et ici la référence du tracker S&P 500 en PEA.
Merci Ludovic pour l’article, ces formules vont être très utiles !
Je pense avoir trouvé 2 coquilles dans l’article, je vous laisse voir si mes remarques sont pertinentes :
1 – Dans le chapitre « Quelle est la performance annualisée de l’indice ? »
Dans la phrase `Valeur initiale / valeur finale = 7965 /491 = 16,20976.`
Je pense que la phrase correcte est `Valeur finale / valeur initiale = 7965 /491 = 16,20976.`
2 – Dans le chapitre « Cas d’un épargnant plaçant 300 euros par mois »
Dans la formule `300 € x (1 + 0,5654 %)240 – 1) / 0,5654 %`, je pense qu’il manque une parenthèse ouvrante.
La formule correcte serait `300 € x ((1 + 0,5654 %)240 – 1) / 0,5654 %`
N’hésitez pas à supprimer mon commentaire si jamais je m’étais totalement trompé 😉
Merci encore
Julien
Bonjour Julien,
Bien vu, merci !
J’ai corrigé ces 2 points 🙂
bonjour Ludovic, encore merci pour vos articles. J’avais connaissance du principe et je l’applique au mieux depuis quelques années mais en rentrant dans le détail je me pose une question par rapport à mon âge. J’ai 35 ans, un bien en LMNP (mon ancienne RP) où j’ai encore 16 mois de crédit à rembourser. Vu mon âge, je suis en mode capitalisation encore pour plusieurs années. Et donc si je veux tirer profit au maximum des intérêts composés pour les 20 prochaines années… ne faudrait il pas vendre cet appartement et placer la somme ensuite sur pea/per/av ?
Bonjour Nicolas,
Si on considère que le marché immobilier est haussier à long terme, l’effet des intérêts composés joue aussi.
Cf l’exemple dans mon commentaire précédent.
Il ne faut pas prendre l’expression « intérêts composés » littéralement. En fait, c’est l’effet capitalisation, et cela marche aussi sans percevoir d’intérêts.
Mais idéalement, vous devez aussi placer hors immobilier, sur les enveloppes capitalisantes (AV / PEA / éventuellement PER). Avec votre effort d’épargne. Car on s’enrichit plus vite en optimisant les 2 leviers : capacité d’épargne et capacité d’emprunt.
Bonjour,
Merci pour vos articles et vos explications très pédagogiques.
Un fond en Euro produit des intérets chaque année (même faible) ce qui permet l’effet boule de neige. Cependant un investissement en actions ou trackers (peu importe le support, assurance vie, PEA, PER) n’a-t-il pas de plus-value uniquement lors de la vente de l’action ou tracker et seulement sous réserve que celle-ci ait pris de la valeur ? Aussi, comment l’effet boule de neige est il possible dans ce cas-là ? Exemple, on investit sur un tracker pendant 20 ans. Merci d’avance de votre réponse.
G. Bernard
Bonjour Bernard,
L’effet boule de neige est à peine perceptible sur un fonds euro ou livret à 2 %, cela fait quasiment une droite linéaire, on est loin de l’exponentielle sauf à placer l’argent plusieurs siècles. Regardez les graphiques ici : https://avenuedesinvestisseurs.fr/introduction-a-lepargne-et-aux-placements/
L’effet boule de neige est bien plus visible en investissant à 7 % comme sur le marché actions et sans vendre, car il faut laisser capitaliser. (Si vous vendez tous les ans en prenant vos plus-values il n’y aura jamais boule de neige ! Donc il faut réinvestir les dividendes, ou encore mieux, choisir des trackers capitalisant !)
On le voit ici sur le S&P 500 : https://avenuedesinvestisseurs.fr/interets-composes-calcul-et-formules/#actions-sp500
Par exemple un portefeuille de 100 k€ en actions à +10 % :
– en N+1 = le portefeuille pèse 110 k€ (+10) ;
– N+2 = 121 k€ (+11) ;
– N+3 = 133,1 k€ (+12,1) ;
– N+4 = 146,41 k€ (+13,31) ;
– N+5 = 161,05 (+14,64) ;
…on commence déjà à voir l’effet boule de neige, la hausse du portefeuille est de plus en plus forte !
(Dans la vraie vie ce sera plus volatil, mais vous avez compris l’idée).
Bonjour Nicolas,
Merci de votre réponse.
Je reformule. J’ai bien compris l’article et vos explications. Ma question est plus simple.
D’où viennent les intérêts permettant l’effet boule de neige chaque année ?
Exemple : j’achète une action de l’entreprise X à 100 euros. Si celle-ci prend 7% par an, elle vaudra donc 107 euros au bout d’un an. Mais pour avoir les intérêts il faut donc la vendre. Or le but est bien d’investir sur le long terme et ne vendre qu’au bout de nombreuses années.
Du coup, d’où viennent les intérêts chaque année ? Des dividendes de l’action ? Si oui, faut il privilégier les actions avec des dividendes plutôt que celles qui auront potentiellement une augmentation de valeur importante ?
Bernard
Bonjour Bernard,
Non, pour avoir les « intérêts » il ne faut pas vendre.
Vous n’avez pas compris le fonctionnement des actions.
On ne touche pas d’intérêts. On s’enrichit par :
1/ capitalisation par la hausse des cours de l’action.
2/ éventuellement distribution de dividendes, mais pas besoin de dividendes pour s’enrichir ! Idéalement on évite même les actions à dividende pour mieux capitaliser (c’est pourquoi je disais de choisir des trackers capitalisant et non distribuant).
Notre article : trackers.
Je vous invite à lire cet article aussi : comment investir en bourse.
Je vais vous donner un exemple immobilier, vous comprendrez peut-être mieux.
Par exemple un appartement de 100 k€ dont la valeur augmente de 10 % par an :
– en N+1 = l’appartement vaut 110 k€ (+10) ;
– N+2 = 121 k€ (+11) ;
– N+3 = 133,1 k€ (+12,1) ;
– N+4 = 146,41 k€ (+13,31) ;
– N+5 = 161,05 (+14,64) ;
…on commence déjà à voir l’effet boule de neige, la hausse de la valeur de l’appartement est de plus en plus forte !
Et pourtant vous n’avez pas touché de loyer sur votre appartement. Vous vous êtes seulement enrichi par la hausse de sa valeur.
Comme pour les actions.
Sauf qu’avec des actions, dans x années, vous pourrez décider de vendre une partie tous les ans en guise de revenus passifs (sur un rythme de 4-5 % par an par exemple pour que le portefeuille garde sa valeur). Alors qu’un appartement, vous ne pouvez pas en vendre un petit bout tous les ans.
Bonjour Nicolas,
Je suis également perdu comme Bernard, concernant les intérêts composés sur des actions ou ETF.
Si par exemple j’achetais une action Amazon en 2019 à 100 USD, elle a pas mal fluctuée depuis mais finalement en 2023, soit 4 ans plus tard, cette action est revenu à 100 USD.
Pourtant l’action est montée à environ 170 USD pendant 2 ans durant cette période.
Au final, où sont les soit disant intérêts composés ? on se retrouve à l’identique d’un nouvel acheteur d’une action en 2023.
Je ne demande qu’à comprendre cette logique d’intérêts composés…
Merci d’avance
Bonjour Grégory,
Vous considérez une seule action, il vaut mieux considérer un ETF et sur le long terme (pas 4 ans, plus de 10 ans).
Quand bien même, l’action Amazon n’a pas fait du surplace, vous n’avez pas compté les dividendes réinvestis.
En réinvestissant les dividendes, vous avez de plus en plus d’actions, donc de plus en plus de dividendes, et c’est le cercle vertueux. Regardez une action comme Air Liquide sur 30 ans.
Je vous invite à lire cet article avec ses graphiques : https://avenuedesinvestisseurs.fr/investir-en-evitant-les-biais-comportementaux-des-investisseurs-finance/
Merci Nicolas pour votre réponse.
Cependant, j’ai bien lu l’article proposé et cela ne m’éclaire toujours pas.
Déjà car dans cet article, vous dites je cite : « Certes recevoir des dividendes peut rassurer, comme des revenus passifs. Mais il s’agit également d’un biais psychologique contreproductif ». Bref, on touche des dividendes mais on a presque perdu autant sur l’action donc on stagne… J’en déduit donc qu’il vaut mieux éviter les dividendes.
Si je reprend mon exemple mais en imaginant alors un ETF. Valeur à l’achat 100 euros en 2020. Des montées, des descentes pendant 10 ans pour finir à une valeur de 150 euros. On se dit, ok on est à 5%/an. Mais je n’ai alors que 150 euros alors qu’avec les calculatrices d’intérêt composé, on annonce 164€. Et si la ca continu toujours sur 5%/an pendant 20 ans supplémentaire, j’aurai 250 euros alors qu’on annonce 439€ avec les intérêts composés.
Il y a un élément où je me trompe ?
Merci d’avance Nicolas.
Gregory,
Il ne faut pas choisir des actions simplement parce qu’elles versent un dividende.
C’est un tout.
Le luxe (LVMH, Hermes, Kering…) a été très rentable depuis des décennies alors que ces sociétés versent peu de dividendes (autour de 1-2 % par an de rendement sur dividende).
Idem pour les GAFA.
Les intérêts composés fonctionnent sur du long terme, au moins 10 ans et idéalement X0 années.
On ne fait pas d’observation sur 3 ans.
Et sur un marché global, parce qu’évidemment on regarde des actions en particulier (Orpea par exemple) on trouve toujours des contre-exemples.
Mais évidemment sur un livret ou un fonds euro, avec l’effet cliquet (intérêts définitivement acquis, ils vont composer à coup sûr), le système des intérêts composés est plus clair à comprendre et infaillible.